Australia

Climate change in Moruya, NSW, Australia.

September 11, 2017 — leslie dean brown

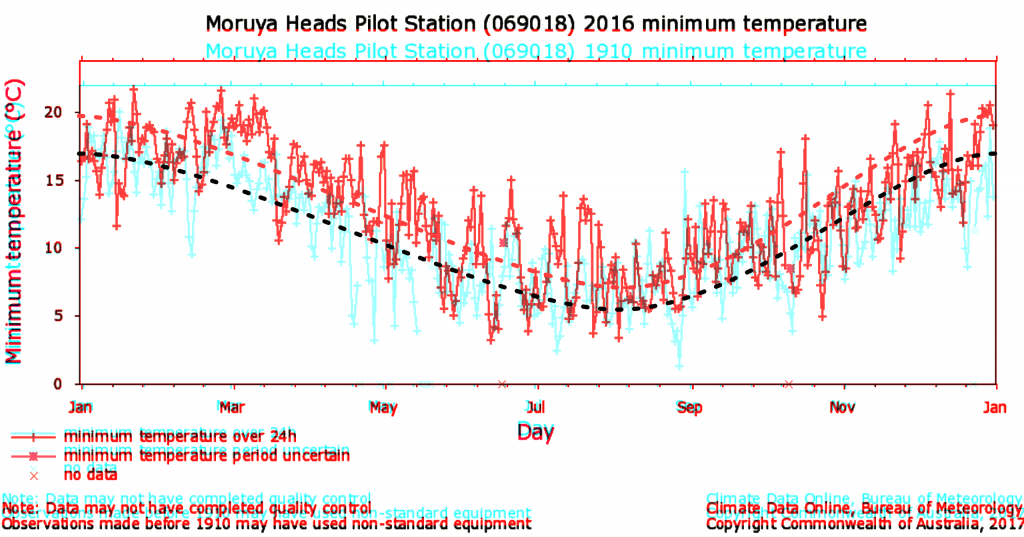
So today I thought I’d share this graph of my nearest weather station in NSW, Australia (well, the second-nearest weather station, because the closest one only has data since the beginning of 2000).

And here it is. Data is from the Australian government Bureau of Meteorology. Moruya heads pilot station. Minimum daily temperatures from 1910 superimpsed with data from 2016. The first year of data compared to the last full year of data. Graphs have been rescaled in the y-axis so that they line up (if they used a consistent scale I wouldn’t have to do this; I think it auto-scales).

Now I have roughly superimposed my own “line of best fit” through both curves (they are both the same height at the beginning and end, as they should be). Yes I eyeballed it. But you can clearly see that the red line is well above the blue line pretty much everywhere.

Now I know this doesn’t “prove” anything because it’s just one weather station of many. And some years are hotter due to the El Niño effect (according to google, both 1900-1901 and 2015-2016 were El Niño periods). But I was curious about something and so I thought I’d personally check it out. [I was originally looking up this very warm day we had on the 3rd of September, 2017 because it was 9°C above average]

Note:

I’ve seen other graphs where people draw their line of best fit and the end tangents don’t match for January and December. I don’t think that is technically correct, because we are looking at continuous trends from month to month and year to year. Where we take the yearly ‘chunk’ of data is kind of irrelevant.

I’ll give you an example: you wouldn’t expect that the temperature for January of 2017 to be significantly different than December of 2016. Likewise, you wouldn’t expect the temperature for December of 2015 to be significantly different than January of 2016. Indeed, we could include these two extra months if we wanted to and look at a 14 month span instead of a 12 month span. But if someone has drawn a wacky curve at the start and finish, and then we include the extra adjoining months, we see that it would be completely wrong.

Therefore, I have inserted the line of best fit through the data so that it matches up at both the start and end of the year. I inserted the minimum number of nodal points (three) and they are ‘symmetrical’. That way, we can expect the temperature fluctuations to continue on from one to the next year and precedes from the last one (without a huge slope at the beginning or end).

“Typical liberal moron”

January 10, 2017 — leslie dean brown

So just today, someone once again called us ‘liberals’ morons. Again.

First of all, I’d like to point out to Americans that in Australia, the liberal party is actually the conservative party. The labor party is the one that swings to the left. So get your facts straight.

I hope you are one of those republicans and you are reading this. I really do. I’ve tried to spam this blog post with conservative keywords in the hope that more of you will find it and actually use a greater proportion of the right hand side of your brain.

Anyway, I think you’ll find that the majority (not all, but most) creative people ARE liberal.

So that means artists, musicians, writers, actors, 3D animators, graphic designers, industrial designers, fashion designers, interior designers, architects, art directors, creative directors, marketing and advertising gurus, chefs, comedians, photographers, hairdressers, dancers … you know… all the people who make life interesting. Not to mention many scientists, psychologists and health care workers as well.

What that means is, who do you actually go to when you do any of the following: read a book; watch movies (other than old westerns); listen to music (anthing but country music that is); buy nice clothes (including designer suits); buy furniture; go out to a restaurant; give birth to a child; watch a comedy; take a taxi; get a haircut; need a lawyer; need a psychologist; go out for a drink at a bar or pub; set foot in a nicely designed home; watch any kind of entertainment.

What music do you listen to when you feel like cheering up? Who do you go to when you want to sell more widgets? Who do you go to when you want advice on branding or corporate identity? How about you stop calling people “liberal morons” eh? Do you not know how to compose an entire sentence without insulting someone? Because it’s becoming tiresome. Really. If anyone has made the Divided States of America, it is you.

I hate to say this, but without liberal people, your society would look a lot like the USSR. You know: communist! Not that there’s anything wrong with that either. It’s just… a bit too depressing by all accounts. [Read more…]

I was worried back in ’92.

October 10, 2016 — leslie dean brown

Yes I first learned about “global warming” in 1991 or 1992.

I think I must have had a smart teacher for the subject called general studies, because she knew about this new topic and warned all of us. She probably heard all about it at the United Nations Conference on Environment and Development (UNCED) aka the Rio de Janeiro Earth Summit. I could tell she was concerned. I can still remember seeing the worry in her eyes way back then.

Also, like a lot of nerdy sciency kids, I already knew about the atmosphere of other planets (like Venus for example). And so I’ve known for a long time that there isn’t really anything (apart from biodiversity feedback loops) stopping this planet from becoming more like either Mars or Venus.

So I began making lifestyle choices back then, when I was 14 or 15 years old. I chose not to drive. I continued to ride my bicycle. I rode it everywhere. In fact I didn’t learn to drive a car until I was 28 years old. Not until I had to. Not until I needed to deliver a lot of bicycles for my business. But eventually, it all caught up with me again. It slowly dawned upon me that I was falling into the trap of becoming just like everyone else again.

We are supposed to be working for a better future. That is why we all work so hard. But if the future is going to be worse, what’s the point?

So now, after almost a decade of driving around, I’m slowly but surely weening myself off of it again.

Later, when I gratuated, I refused to work for oil companies. I was offered a very highly paid job investigating the steel microstructure of crude oil tankers. I just couldn’t do it. So I went straight back to university and did another 5 years there.

Climate scientists are saying now that we are in a “climate emergency”. Look, the coal industry in Australia is saying there is enough coal reserves to last another 365 years. Well okay. But if other planets are anything to go by, this world’s entire fucking oceans could potentially boil right off and disappear into deep space! Melting icecaps will be the least of our worries. Now, while that scenario is never mentioned by climate scientists, that’s what planetary scientists mean when they talk about “a climate system that is out of control”. Are people starting to get it now?

Now I still don’t think people even today fully realise the implications of climate change, 25 years later.

Who are the greenest printers in Australia?

August 15, 2016 — leslie dean brown

I just finished a diploma of graphic design a few months ago. And during a subject called “prepress”, I found out that printing is not the most ecological part of graphic design. In fact traditional printing is not very good for the environment at all. It isn’t all just about the paper they use, but they also use loads and loads of metal printing plates and lots and lots of water.

So I have been shopping around for the most ecological printer for some time now (like 6 months, on and off). And I think I’ve finally found a quality one that is reasonably priced. [Read more…]

What this angry scientist has to say about climate change:

July 1, 2016 — leslie dean brown

Here I go again… why am I angry? Do scientists even get angry? Yes. Yes they do. Well I am angry. Very fucken angry!

I‘m angry at politicians in the mainstream parties. Because they aren’t doing enough to mitigate an environmental catastrophe. Most politicians today only care about one thing: money. The economy. Whoop-de-doo.

Scientists, if you remember from highschool, are the clever people. They are the nerdy ones with poor social skills. You’d think most countries would be run by the smartest of individuals. Are they? No. See, I think that’s where we’re going wrong. Our countries are run by politicians.

Likewise, I am angry at climate change deniers. Because they are now claiming that “climate change is a government conspiracy” (right, well if that is true it has to be the dumbest conspiracy theory I have ever heard, because the governments are the ones who support burning coal for fuck’s sake!).

Actually, I lie. Half of it is worry, not anger. For example, what’s actually worrying is that some people think an average temperature increase of a couple of degrees in only a few decades is at all “natural”. What’s worrying is that some people still don’t seem to grasp the concept of “rate of change”. I have seen on LinkedIn that the biggest climate change deniers are frequently either working for oil companies, have a vested interest in contruction, or are simply “uneducated fools”.

I find some people’s responses to climate change infuriating. Scientists are (mostly) a VERY clever bunch of people. If climate scientists are ringing alarm bells and making videos like this one, it’s enough to make me pay attention and completely change my lifestyle.

Right. I’ll say that again, but in a different way, because it bears repeating. Because I know that people skim read things. When the leading climate scientist, James Hansen, says (back in 2012 mind you) that “we have a climate emergency“, well, it’s enough to make me sell my vehicle. It’s enough to make me think up a new career choice, about how I can make the world a better place for future generations to come…

In science, we have to have a kind of ‘faith’ too. Scientists have faith in other scientists. We mutually respect each others’ fields of expertise. If I were to say, as a materials scientist, that magnesium has a hexagonal close packed atomic structure, I would hope the other scientists would give me the benefit of the doubt about that. And that is how the whole science community works. Things are checked and rechecked. Publications are reviewed. These people are working on these problems their whole lives. [Read more…]